Une densité sur $\mathbb{R}$ est une fonction qui vérifie 3 conditions: - Cette fonction doit être continue sur $\mathbb{R}$. - Cette fonction doit être positive sur $\mathbb{R}$. - L' aire sous la courbe de cette fonction sur l'intervalle $\mathbb{R}$ doit être égale à 1 unité d'aire.. La fonction de densité de probabilité (PDF) est une équation qui représente la loi de probabilités d'une variable aléatoire continue. Par exemple, une machine qui découpe des bouchons pour des bouteilles de vin fabrique des bouchons de différents diamètres. Dans la carte barre suivante des diamètres de bouchon, chaque barre.

TS Cours Lois de probabilités à densité Maths

fonction de densité de probabilité loi normale
fonction de densité de probabilité du diamètre des bulles calculés à la... Download Scientific

6 Représentation de deux fonctions de densité de probabilité de... Download Scientific Diagram

loi de densité de probabilité exo bac loi normale YouTube

Densité de probabilité , volumique et radiale, de présence de l électron YouTube
8. (a) Fonction de densité de probabilité normale des log 10 (C) pour... Download Scientific
41 Courbes de densité de probabilité calculées en fonction du nombre... Download Scientific

Lois à densité Loi normale Cours AlloSchool

10. La fonction de densité de probabilité de CRR et CSR à z=3m Download Scientific Diagram

Densité de probabilité répartie et cumulée. Figure 226 Température... Download Scientific
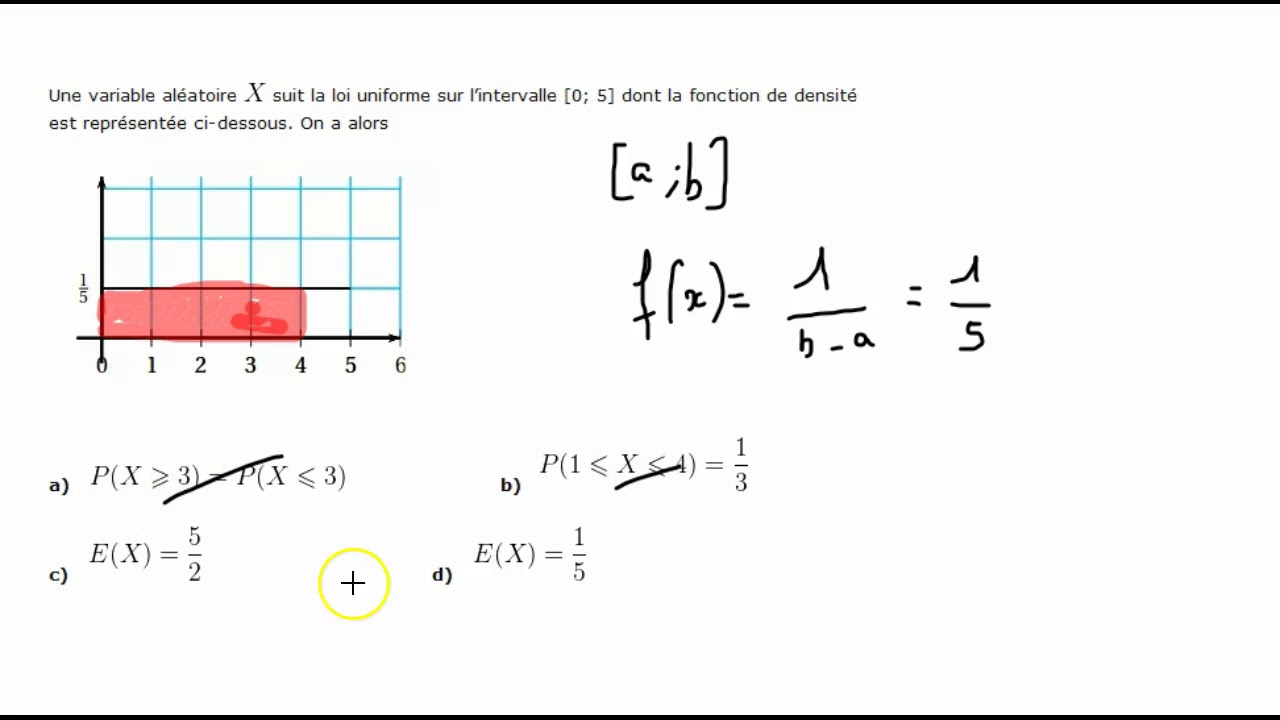
fonction de densité de probabilité exo bac loi uniforme YouTube
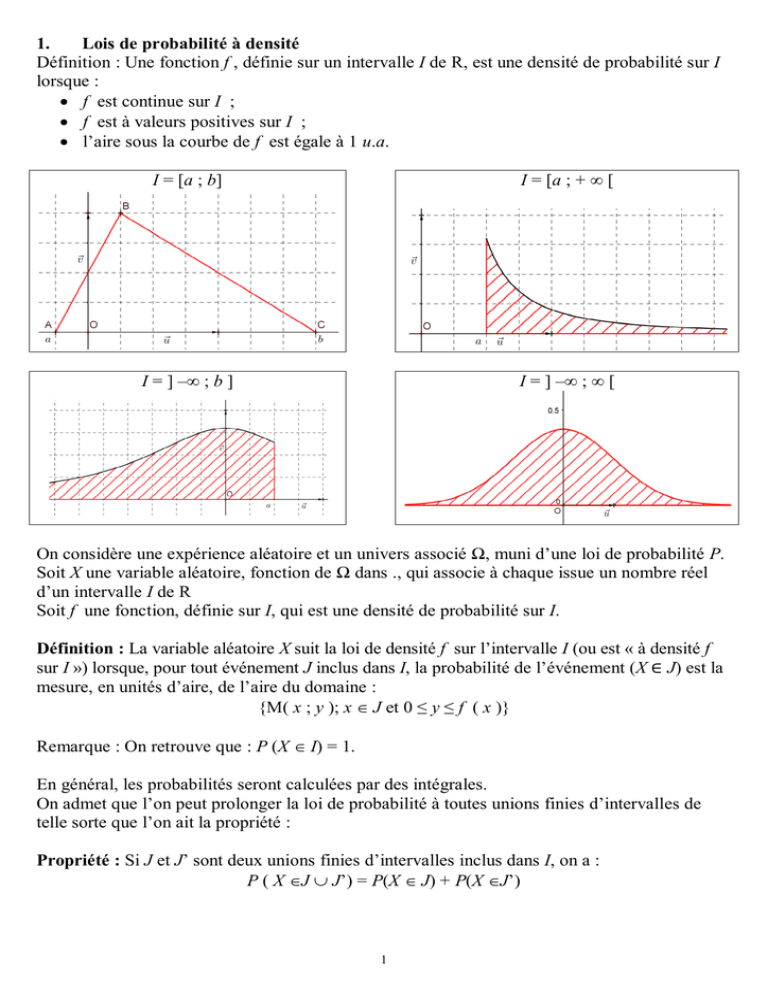
1. Lois de probabilité à densité Définition Une fonction

matplotlib Python Matplotlib normalisation de l'axe lors de la représentation d'une

loi de probabilité à densité 8 approche de la loi normale YouTube

Fonction de densité de probabilité conditionnelle p ξr (ξr), avec ∆ f... Download Scientific

3Carte SiZer et fonction de probabilité de densité. La carte SiZer est... Download Scientific

fonction de densité de probabilité conjointe

Fonctions de densité de probabilité (PDF) des incréments de courant δI... Download Scientific
Graphe illustrant la fonction de probabilité de densité de la phase... Download Scientific Diagram
pour tout réel k si X est une loi à densité. Du coup on peut en déduire certaines choses : P ( X ≤ b) = P ( X < b) P ( X ≥ a) = P ( X > a) On peut faire de même quand on a P (a < X < b). ATTENTION ! Toutes ces formules ne sont vraies que pour les lois à densité, comme tout ce qui se trouve sur cette page.. Soit X une variable aléatoire continue à valeurs dans un intervalle I muni d'une fonction densité de probabilité f. Alors : (P 1) Probabilité en un point : Pour tout réel c ∈ I : P ( { c }) = P ( X = c) = 0. (P 2) Les bornes n'ont pas d'importance. Pour tous nombres réels c, d ∈ I :