el que se designan las dos componentes de cada número complejo. Cada z∈C seexpresademaneraúnicacomo z = x +iy con x,y∈R,donde i=(0,1). Se dice que x es la parte real del número complejo z, y escribimos x = Rez, mientras que y es la parte imaginaria de z que se denota por y = Imz. En particular, z ∈ R si y sólo si, Imz = 0.. Problema 1. Calcular el módulo y el argumento de los siguientes números complejos: Solución. 3. Conjugado. Dado un número complejo en su forma binómica z = a + bi z = a + b i, se define su conjugado como. Interpretación geométrica. Si representamos un complejo y su conjugado, son simétricos respecto del eje horizontal:

Elecciones 10N Voto en blanco, nulo y abstención, ¿a quién beneficia

ARGUMENTO DE UN NÚMERO COMPLEJO YouTube

Division De Numeros Complejos Ejemplos Resueltos Nuevo Ejemplo

siendo ‘‘S'', ‘‘C’' y‘‘R''lo conocido para un ángulo no nulo reduce

Números ComplejosParte real e imaginariaOpuesto y Conjugado YouTube

Tanque Gerente Contradicci N Calcular El Argumento De Un Numero Hot

En cada literal se da un vector no nulo aER2. Obtén la recta L que pasa

Ejemplos De Numeros Puros

LO QUE ES NULO NO PRODUCE EFECTO ALGUNO YouTube

Descubre la definición del ángulo nulo en geometría CFN

Lesson Video El argumento de un número complejo Nagwa

MAGIC PL/SQL ORACLE Función Cual es Nulo?

En cada literal se da un vector no nulo à ER Obtén la recta L que pasa

Campo nulo

Argumento de un número complejo YouTube

Argumento Nulo YouTube

Las 10 mentiras y verdades sobre el voto nulo

Permitir valores nulos en SQL Server (CREATE TABLE y ALTER TABLE) DBA
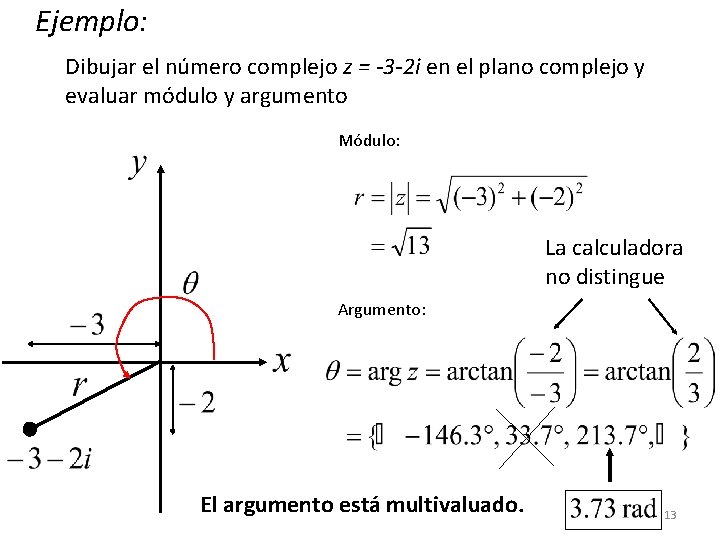
Modulo Y Argumento De Un Numero Complejo Modulo

siendo s y C lo convencional para un ángulo no nulo simplificar = 3s_2c
Luego, la suma equivale a sumar las partes real e imaginaria de cada complejo. Ejemplo 2. Si z = ¡ 1+3. i y w = 2 ¡ 4. i, entonces z + w = (¡ 1+2)+(3 ¡ 4) i = 1 ¡i: b) Producto: Para multiplicar. z = a + bi. por. w = c + di, haremos el c¶alculo. z ¢w = (a + bi) ¢ (c + di) = ac + adi + bci + bdi. 2. Para tener deflnido completamente el.. tiene elemento neutro, y es tal que cada número complejo tiene un elemento simétrico, que es su opuesto. Además, como caso particular del citado teorema, se constata fácilmente que el producto de complejos por escalares reales satisface las siguientes propiedades: